机器人刚度建模
机器人在进行曲面加工时,铣削加工的铣削力数值较大且方向经常变化,机器人各个关节在抵御铣削力时容易发生形变,累积到末端产生变形误差,从而使机器人加工精度下降。因此,如何提高机器人的刚度性能是目前研究的重点。
1 机器人雅可比矩阵
除了关节角度和机器人末端执行器位置之间的关系外,还需要研究关节和末端执行器速度之间的关系。由机器人运动学公式,当给定一组关节角θ = [ θ 1 , θ 2 , θ 3 , θ 4 , θ 5 , θ 6 ] T \boldsymbol{\theta }=\left[ \theta _1,\theta _2,\theta _3,\theta _4,\theta _5,\theta _6 \right] ^{\mathrm{T}} θ = [ θ 1 , θ 2 , θ 3 , θ 4 , θ 5 , θ 6 ] T
X = F ( θ ) \boldsymbol{X}=F\left( \boldsymbol{\theta } \right)
X = F ( θ )
其中,X = [ X , Y , Z , A , B , C ] T \boldsymbol{X}=\left[ X,Y,Z,A,B,C \right] ^{\mathrm{T}} X = [ X , Y , Z , A , B , C ] T
V = X ˙ = J ( θ ) θ ˙ \boldsymbol{V}=\dot{\boldsymbol{X}}=\boldsymbol{J}\left( \boldsymbol{\theta } \right) \dot{\boldsymbol{\theta}}
V = X ˙ = J ( θ ) θ ˙
式中,$\boldsymbol{J}\left( \boldsymbol{\theta } \right) $为雅可比矩阵。
一般情况下,雅可比矩阵通过矢量差乘积法、微分变换法得到。而使用指数积公式表示正运动学,可以更加明确、优雅的推导出雅可比矩阵。在机器人正运动学的指数积公式下,末端的速度$\left[ \boldsymbol{V} \right] $的表达式为:
[ V ] = T ˙ T − 1 = ∑ i = 1 6 ( ∂ T ∂ θ i θ ˙ i ) T − 1 = ∑ i = 1 6 ( ∂ T ∂ θ i T − 1 ) θ ˙ i \left[ \boldsymbol{V} \right] =\dot{\boldsymbol{T}}\boldsymbol{T}^{-1}=\sum_{i=1}^6{\left( \frac{\partial \boldsymbol{T}}{\partial \boldsymbol{\theta }_i}\dot{\boldsymbol{\theta}}_i \right)}\boldsymbol{T}^{-1}=\sum_{i=1}^6{\left( \frac{\partial \boldsymbol{T}}{\partial \boldsymbol{\theta }_i}\boldsymbol{T}^{-1} \right)}\dot{\boldsymbol{\theta}}_i
[ V ] = T ˙ T − 1 = i = 1 ∑ 6 ( ∂ θ i ∂ T θ ˙ i ) T − 1 = i = 1 ∑ 6 ( ∂ θ i ∂ T T − 1 ) θ ˙ i
带入机器人正运动学公式,并使用伴随映射将上式写成向量形式,即:
V = ξ 1 ⏟ J 1 θ ˙ 1 + A d e ξ 1 θ 1 ( ξ 2 ) ⏟ J 2 θ ˙ 2 + A d e ξ 1 θ 1 e ξ 2 θ 2 ( ξ 3 ) ⏟ J 3 θ ˙ 3 + ⋯ \boldsymbol{V} = \underset{\boldsymbol{J}_1}{\underbrace{\boldsymbol{\xi}_1}} \dot{\theta}_1 + \underset{\boldsymbol{J}_2}{\underbrace{Ad_{e^{\boldsymbol{\xi}_1\theta_1}} \left( \boldsymbol{\xi}_2 \right)}} \dot{\theta}_2 + \underset{\boldsymbol{J}_3}{\underbrace{Ad_{e^{\boldsymbol{\xi}_1\theta_1}e^{\boldsymbol{\xi}_2\theta_2}} \left( \boldsymbol{\xi}_3 \right)}} \dot{\theta}_3 + \cdots
V = J 1 ξ 1 θ ˙ 1 + J 2 A d e ξ 1 θ 1 ( ξ 2 ) θ ˙ 2 + J 3 A d e ξ 1 θ 1 e ξ 2 θ 2 ( ξ 3 ) θ ˙ 3 + ⋯
V = [ J 1 J 2 ⋯ J 6 ] [ θ ˙ 1 θ ˙ 2 ⋮ θ ˙ 6 ] = J ( θ ) θ ˙ \boldsymbol{V}=\left[ \begin{matrix} \boldsymbol{J}_1& \boldsymbol{J}_2& \cdots& \boldsymbol{J}_6\\\end{matrix} \right] \left[ \begin{array}{c} \dot{\theta}_1\\ \dot{\theta}_2\\ \vdots\\ \dot{\theta}_6\\\end{array} \right] =J\left( \boldsymbol{\theta } \right) \dot{\boldsymbol{\theta}}
V = [ J 1 J 2 ⋯ J 6 ] θ ˙ 1 θ ˙ 2 ⋮ θ ˙ 6 = J ( θ ) θ ˙
式中,对于任意ξ ∈ R 6 \boldsymbol{\xi }\in \boldsymbol{R}^6 ξ ∈ R 6
ξ ′ = A d T ( ξ ) = [ R 0 [ P ] R R ] ξ \boldsymbol{\xi }^{\prime}=Ad_{\boldsymbol{T}}\left( \boldsymbol{\xi } \right) =\left[ \begin{matrix} \boldsymbol{R}& 0\\ \left[ \boldsymbol{P} \right] \boldsymbol{R}& \boldsymbol{R}\\\end{matrix} \right] \boldsymbol{\xi }
ξ ′ = A d T ( ξ ) = [ R [ P ] R 0 R ] ξ
由虚功原理,关节处的功率消耗为机器人运动的功率消耗和末端执行器的功率消耗之和,假设机器人处于静平衡状态,没有用于机器人运动的功率消耗,关节处功率消耗等于末端执行器的功率消耗,用公式表示为:
τ T θ ˙ = F T V \boldsymbol{\tau }^{\mathrm{T}}\dot{\boldsymbol{\theta}}=\boldsymbol{F}^{\mathrm{T}}\boldsymbol{V}
τ T θ ˙ = F T V
式中,τ \boldsymbol{\tau } τ θ ˙ \dot{\boldsymbol{\theta}} θ ˙ F 为末端所受外力,V 为末端空间速度,利用公式V = J ( θ ) θ ˙ \boldsymbol{V}=\boldsymbol{J}\left( \boldsymbol{\theta } \right) \dot{\boldsymbol{\theta}} V = J ( θ ) θ ˙
τ = J T ( θ ) F \boldsymbol{\tau }=\boldsymbol{J}^{\mathrm{T}}\left( \boldsymbol{\theta } \right) \boldsymbol{F}
τ = J T ( θ ) F
上式表示的是关节力矩与末端所受外力之间的关系,若一个外力作用在末端器上以平衡各关节力矩,使用上式便可用于计算该力矩,以产生反作用力使机器人处于平衡状态。J T \boldsymbol{J}^{\mathrm{T}} J T
2 机器人刚度建模
KUKA KR60-3机器人臂架的刚性远大于关节的刚性,因此我们将仅考虑关节柔性对末端的偏移造成的影响,同时将关节的刚度映射至机器人末端的刚度。将各个关节间的驱动装置的刚度用一个弹簧来近似,各关节的受外力矩τ θ
τ = K θ Δ θ \boldsymbol{\tau }=\boldsymbol{K}_{\theta}\varDelta \boldsymbol{\theta }
τ = K θ Δ θ
式中,K θ K_{\theta} K θ
由前文机器人力雅可比矩阵可知外力与关节力矩的关系,带入上述公式为:
τ = J T ( θ ) F \boldsymbol{\tau }=\boldsymbol{J}^{\mathrm{T}}\left( \boldsymbol{\theta } \right) \boldsymbol{F}
τ = J T ( θ ) F
末端变形为:
Δ X = J Δ θ \varDelta \boldsymbol{X}=\boldsymbol{J}\varDelta \boldsymbol{\theta }
Δ X = J Δ θ
根据胡克定律,机器人末端执行器在空间中受到外力发生变形,可以使用公式表示为:
F = K Δ X = K J Δ θ \boldsymbol{F}=\boldsymbol{K}\varDelta \boldsymbol{X}=\boldsymbol{KJ}\varDelta \boldsymbol{\theta }
F = K Δ X = KJ Δ θ
式中,F X
将上述公式联合可得:
K = J − T K θ J − 1 \boldsymbol{K}=\boldsymbol{J}^{-\mathrm{T}}\boldsymbol{K}_{\theta}\boldsymbol{J}^{-1}
K = J − T K θ J − 1
式中,J
当机器人处于奇异形位,雅可比矩阵不可逆,导致上述公式不成立,尽管知道末端受力也无法预测末端变形情况。因此,在加工过程中需要避免使机器人处于奇异形位。关节刚度矩阵为对角矩阵,由矩阵的运算性质可知,末端笛卡尔刚度矩阵K
K = [ k 11 k 12 ⋯ k 16 k 21 k 22 ⋯ k 26 ⋮ ⋮ ⋱ ⋮ k 61 k 61 ⋯ k 66 ] \boldsymbol{K}=\left[ \begin{matrix} k_{11}& k_{12}& \cdots& k_{16}\\ k_{21}& k_{22}& \cdots& k_{26}\\ \vdots& \vdots& \ddots& \vdots\\ k_{61}& k_{61}& \cdots& k_{66}\\\end{matrix} \right]
K = k 11 k 21 ⋮ k 61 k 12 k 22 ⋮ k 61 ⋯ ⋯ ⋱ ⋯ k 16 k 26 ⋮ k 66
3 刚度性能指标
上述运算涉及雅可比矩阵的求逆,这会导致运算过程中出现误差,尤其是在靠近机器人奇异形位的情况,针对上述问题,定义柔度矩阵为:
C = K − 1 = J K θ − 1 J T \boldsymbol{C}=\boldsymbol{K}^{-1}=\boldsymbol{JK}_{\theta}^{-1}\boldsymbol{J}^{\mathrm{T}}
C = K − 1 = JK θ − 1 J T
由公式可以看出,机器人末端笛卡尔柔度矩阵的计算未涉及到雅可比矩阵的求逆运算。机器人末端变形Δ X \Delta \boldsymbol{X} Δ X F Δ X = C F \Delta \boldsymbol{X}=\boldsymbol{CF} Δ X = CF
[ d δ ] = [ C f d C f δ C m d C m δ ] [ F M ] \left[ \begin{array}{c} \boldsymbol{d}\\ \boldsymbol{\delta }\\\end{array} \right] =\left[ \begin{matrix} \boldsymbol{C}_{fd}& \boldsymbol{C}_{f\delta}\\ \boldsymbol{C}_{md}& \boldsymbol{C}_{m\delta}\\\end{matrix} \right] \left[ \begin{array}{c} \boldsymbol{F}\\ \boldsymbol{M}\\\end{array} \right]
[ d δ ] = [ C fd C m d C f δ C m δ ] [ F M ]
式中,C f d \boldsymbol{C}_{fd} C fd C m δ \boldsymbol{C}_{m\delta} C m δ C f δ \boldsymbol{C}_{f\delta} C f δ C m d \boldsymbol{C}_{md} C m d
在实际加工过程中,末端的扭转变形与平移变形相比可以忽略不计,为了简化问题,只考虑末端的平移变形,将6 × 6 6\times 6 6 × 6 3 × 3 3\times 3 3 × 3
刚度是影响机器人末端变形的重要因素,为了研究刚度对机器人铣削加工变形的影响,需要引入一个刚度性能指标对机器人的刚度进行评价,而柔度矩阵C
d = C f d f \boldsymbol{d}=\boldsymbol{C}_{fd}\boldsymbol{f}
d = C fd f
其中,f f f
设机器人末端受外力的平移变形为单位向量:
∥ d ∥ 2 = d T d = f T C f d T C f d f = 1 \left\| \boldsymbol{d} \right\| ^2=\boldsymbol{d}^{\mathrm{T}}\boldsymbol{d}=\boldsymbol{f}^{\mathrm{T}}{\boldsymbol{C}_{fd}}^{\mathrm{T}}\boldsymbol{C}_{fd}\boldsymbol{f}=1
∥ d ∥ 2 = d T d = f T C fd T C fd f = 1
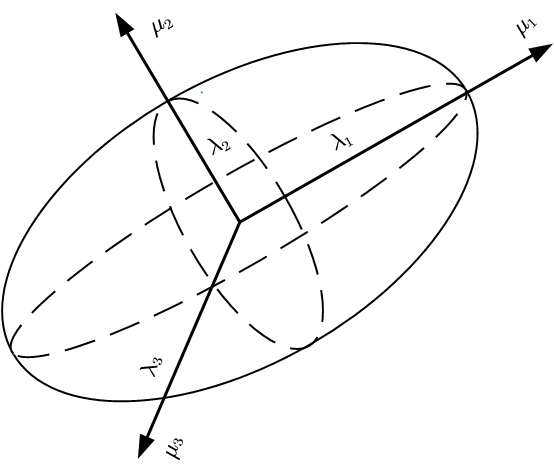
上述公式定义了一个三维笛卡尔柔度椭球,如图所示。半长轴长度为λ 1 、 λ 2 、 λ 3 λ_1、λ_2、λ_3 λ 1 、 λ 2 、 λ 3 λ 1 、 λ 2 、 λ 3 λ_1、λ_2、λ_3 λ 1 、 λ 2 、 λ 3 C f d T C f d C_{fd}^TC_{fd} C fd T C fd V C f d T C f d C_{fd}^TC_{fd} C fd T C fd k k k
k = λ 1 λ 2 λ 3 = d e t ( C f d T C f d ) k=\sqrt{\lambda _1\lambda _2\lambda _3}=\sqrt{det\left( {\boldsymbol{C}_{fd}}^{\mathrm{T}}\boldsymbol{C}_{fd} \right)}
k = λ 1 λ 2 λ 3 = d e t ( C fd T C fd )
以下为机器人刚度性能指标计算代码:
def Stiffness (thetalist ): Jb = mr.JacobianBody(Blist, thetalist) try : A = np.dot(Jb, Jb.T) K_theta = np.diag([5.7e7 , 6.2e6 , 1.2e7 , 2.1e6 , 2.3e6 , 2.3e6 ]) StiffnessMatrix = np.linalg.inv(Jb).T @ K_theta @ np.linalg.inv(Jb) transStiffnessMatrix = StiffnessMatrix[3 :6 , 0 :3 ] ComplianceMatrix = Jb @ np.linalg.inv(K_theta) @ Jb.T transComplianceMatrix = ComplianceMatrix[3 :6 , 0 :3 ] A = np.dot( transComplianceMatrix.T, transComplianceMatrix) eigenvalue, featurevector = np.linalg.eig(A) except : print ('该姿态处于奇异形位!' ) return eigenvalue
在实际铣削加工中,加工效果的评价往往是针对整个曲面或者某一个区域,而不是某一个加工点。机器人刚度评价指标是对某一个机器人姿态进行评价,一个位姿的刚度良好并不能代表整个区域的刚度符合要求,因而需要提出一个评价区域的整体刚度的指标,使区域整体符合加工需求。使用加工区域内所有轨迹点刚度指标的统计特征整体刚度指标H 来描述区域加工效果,整体刚度指标H 体现的是全局的加工效果,而不是针对某个点,可以使姿态优化更为全面,使整个区域满足优化目标。
{ H = r μ + ( 1 − r ) σ μ = ∑ i = 1 N k i N σ = 1 N ∑ i = 1 N ( k i − μ ) 2 \left\{ \begin{array}{l} H=r\mu +\left( 1-\mathrm{r} \right) \sigma\\ \mu =\frac{\sum\nolimits_{i=1}^N{k_i}}{N}\\ \sigma =\sqrt{\frac{1}{N}\sum\nolimits_{i=1}^N{(k_i-\mu )^2}}\\\end{array} \right.
⎩ ⎨ ⎧ H = r μ + ( 1 − r ) σ μ = N ∑ i = 1 N k i σ = N 1 ∑ i = 1 N ( k i − μ ) 2
其中,k i k_i k i i 个轨迹时的刚度评价指标,r 为平均值$\mu 和标准差 和标准差 和标准差
对于给定加工曲面,其相邻的刀位点对应的理想最优姿态都比较相近,因为相邻的刀位点具有接近的位置和姿态,其对应的机器人加工姿态也是相似的。对于相对简单,变化平缓的曲面,可以使用相同的优化参数,而对于曲率大、法向变化频繁的曲面,可以对其进行分割,使用不同参数进行加工,提高加工性能的同时降低计算时间。
基于谱聚类的区域分割方法
首先使用UG软件生成加工轨迹,如图3-12所示。机器人的加工性能与铣削力和加工姿态相关,而铣削力和姿态又由加工轨迹决定。因此,相邻轨迹点的机器人姿态和所受铣削力是接近的,其所对应最优加工参数也应该是相近的。由此,可以使用聚类算法根据加工轨迹点对应的机器人刚度性能将曲面划分为不同的子区域,每个子区域内加工点使用同一组优化参数,提高轨迹优化的效率。
对于待分割的轨迹点,通过机器人运动学逆解,求解刀具轨迹点对应的机器人关节角,计算机器人当前姿态下刚度椭球的各长半轴长度λ 1 、 λ 2 、 λ 3 λ_1、λ_2、λ_3 λ 1 、 λ 2 、 λ 3 V i = ( x i , y i , z i , λ 1 , λ 2 , λ 3 ) V_i=(x_i, y_i, z_i,λ_1, λ_2, λ_3) V i = ( x i , y i , z i , λ 1 , λ 2 , λ 3 ) G = ( V , E ) G=(V,E) G = ( V , E ) E E E V i V_i V i w i j w_{ij} w ij
w i , j = e − d i s t ( i , j ) 2 σ 2 w_{i,j}=e^{\frac{-dist\left( i,j \right)}{2\sigma ^2}}
w i , j = e 2 σ 2 − d i s t ( i , j )
其中,d i s t i j dist_{ij} d i s t ij
d i s t i , j = ∣ V i − V j ∣ dist_{i,j}=\left| \boldsymbol{V}_i-\boldsymbol{V}_j \right|
d i s t i , j = ∣ V i − V j ∣
其中,$\sigma 是一个比例参数,如果 是一个比例参数,如果 是一个比例参数,如果 太小了,可能会分离本应该属于同一子区域的点,如果 太小了,可能会分离本应该属于同一子区域的点,如果 太小了,可能会分离本应该属于同一子区域的点,如果 太大了,可能会将不同子区域中的点错误的聚在一起。在本文中,根据以前的研究经验 [ 65 ] ,选择设置 太大了,可能会将不同子区域中的点错误的聚在一起。在本文中,根据以前的研究经验[65],选择设置 太大了,可能会将不同子区域中的点错误的聚在一起。在本文中,根据以前的研究经验 [ 65 ] ,选择设置
σ = 1 n 2 ∑ ( i ⩽ i , j ⩽ n ) d i s t i , j \sigma =\frac{1}{n^2}\sum{_{\left( i\leqslant i,j\leqslant n \right)}dist_{i,j}}
σ = n 2 1 ∑ ( i ⩽ i , j ⩽ n ) d i s t i , j
通过公式(3-21)构建一个的n × n n\times n n × n W n 为轨迹点数量:
W = [ l w 11 ⋯ w 1 n ⋮ ⋱ ⋮ w n 1 ⋯ w n n ] \boldsymbol{W}=\left[ \begin{matrix}{l} w_{11}& \cdots& w_{1n}\\ \vdots& \ddots& \vdots\\ w_{n1}& \cdots& w_{nn}\\\end{matrix} \right]
W = l w 11 ⋮ w n 1 ⋯ ⋱ ⋯ w 1 n ⋮ w nn
进一步地,使用谱聚类算法对所构建的相似度矩阵进行处理,选择将轨迹分割为5个子区域,得到最终的分类结果,轨迹聚类结果如图所示。
以下为基于刚度性能的加工轨迹分割:
import numpy as npfrom sklearn.cluster import KMeans,spectral_clusteringimport matplotlib.pyplot as pltfrom kine import PoeIkinefrom kine import PoeFkinefrom CLSHander import clsTransimport mathdef dis (X1, X2 ): x1 = X1.copy() x2 = X2.copy() geoDist = np.linalg.norm(x1[0 :3 ] - x2[0 :3 ]) stiffnessDist = np.linalg.norm(x1[3 ] - x2[3 ]) return geoDist,stiffnessDist def affinity_matrix (X ): disSum = np.zeros([len (X),len (X)]) geoMatrix = np.zeros([len (X),len (X)]) stiffMatrix = np.zeros([len (X),len (X)]) for i in range (len (X) - 1 ): for j in range (i + 1 , len (X)): geoDist, stiffnessDist = dis(X[i], X[j]) geoMatrix[i,j] = geoMatrix[j,i] = geoDist stiffMatrix[i,j] = stiffMatrix[j,i] = stiffnessDist geoMatrix = geoMatrix / np.mean(geoMatrix) angMatrix = stiffMatrix / np.mean(stiffMatrix) disSum = geoMatrix + stiffMatrix sigma = 0.7 A = np.exp(-disSum / (2 * sigma ** 2 )) return A def unnormalized_laplacian (adj_matrix ): R = np.sum (adj_matrix, axis=1 ) degreeMatrix = np.diag(R) return degreeMatrix - adj_matrix def normalized_laplacian (adj_matrix ): R = np.sum (adj_matrix, axis=1 ) R_sqrt = 1 /np.sqrt(R) D_sqrt = np.diag(R_sqrt) I = np.eye(adj_matrix.shape[0 ]) return I - np.matmul(np.matmul(D_sqrt, adj_matrix), D_sqrt) def get_eigen (L, num_clusters ): eigenvalues, eigenvectors = np.linalg.eigh(L) best_eigenvalues = np.argsort(eigenvalues)[0 :num_clusters] U = np.zeros((L.shape[0 ], num_clusters)) U = eigenvectors[:, best_eigenvalues] return U def cluster (data, num_clusters ): data = np.array(data) W = affinity_matrix(data) L = normalized_laplacian(W) eigenvectors = get_eigen(L, num_clusters) clf = KMeans(n_clusters=num_clusters) s = clf.fit(eigenvectors) label = s.labels_ return label def plotRes (data, clusterResult, clusterNum ): """ 结果可似化 : data: 样本集 : clusterResult: 聚类结果 : clusterNum: 聚类个数 :return: """ fig1 = plt.figure() ax1 = fig1.add_subplot(projection='3d' ) ax1.axis("off" ) fig2 = plt.figure() ax2 = fig2.add_subplot(projection='3d' ) ax2.plot(data[:,0 ], data[:,1 ], data[:,2 ], c="red" , marker='.' ) ax2.axis("off" ) n = len (data) scatterColors = ['black' , 'blue' , 'red' , 'yellow' , 'green' , 'purple' , 'orange' ] for i in range (clusterNum): color = scatterColors[i % len (scatterColors)] x1 = [] y1 = [] z1 = [] for j in range (n): if clusterResult[j] == i: x1.append(data[j, 0 ]) y1.append(data[j, 1 ]) z1.append(data[j, 2 ]) ax1.plot(x1, y1, z1, c=color, marker='.' ) plt.subplots_adjust(top=1 , bottom=0 , left=0 , right=1 , hspace=0 , wspace=0 ) def normalization (pos ): data = np.copy(pos) length = len (data[0 ]) for i in range (length): data[:, i] = (data[:, i] - np.min (data[:, i])) / ( np.max (data[:, i]) - np.min (data[:, i]) ) return data def clusterMain (data,cluster_num ): pos = data.copy() for i in range (len (pos)): pos[i] = pos[i] vectorList = [] initial = np.array([3.50 / 180 * math.pi, -70.43 / 180 * math.pi, 125.62 / 180 * math.pi, 6.41 / 180 * math.pi, -55.40 / 180 * math.pi, -2.67 / 180 * math.pi]) for i in range (len (pos)): position = np.array(pos[i][0 :3 ]) Tmatrix = PoeIkine.RpToMatrix(pos[i]) [theta,success] = PoeIkine.ikine(Tmatrix,initial) translation_vector,_ = PoeFkine.StiffnessMatrix(theta) vector = np.append(position,translation_vector) vectorList.append(vector) initial = theta data = np.array(vectorList) data = normalization(data) label = cluster(data, cluster_num) plotRes(np.array(vectorList), label, cluster_num) return label def main (): xpath = '../data/clsdata/曲面轨迹精密.cls' workpieceFrame = np.array([1545.32 ,-49.85 ,730.99 ,0 ,0 ,0 ]) pos = clsTrans.cls_Main(xpath, workpieceFrame) label = clusterMain(pos,4 ) plt.show()