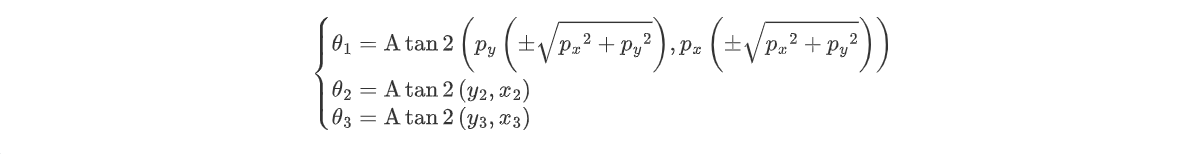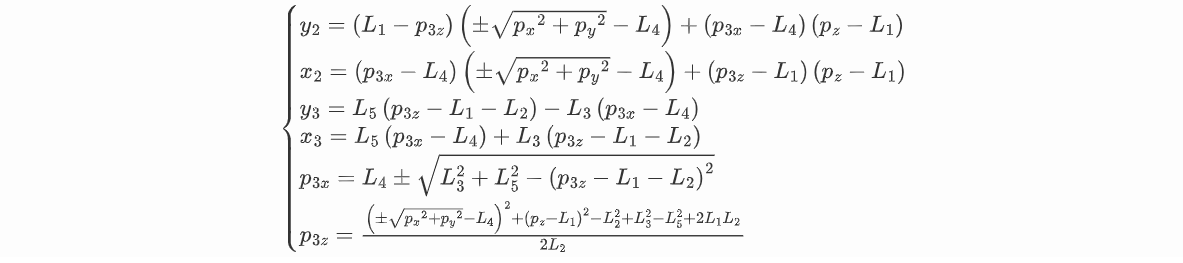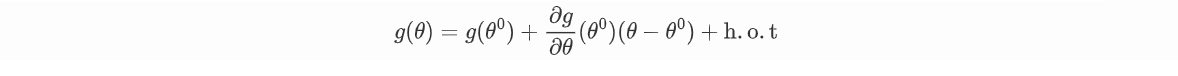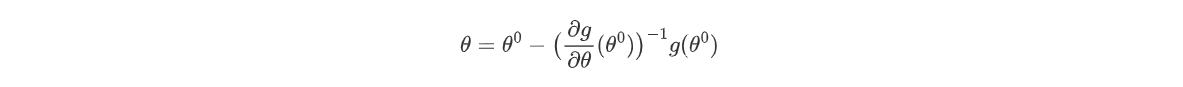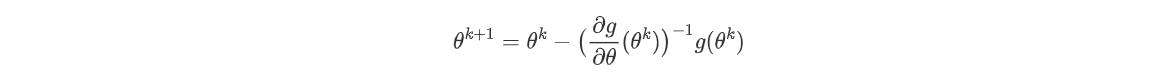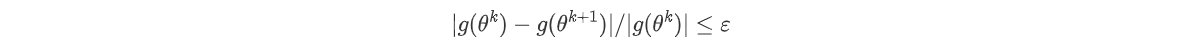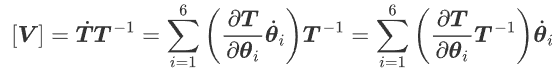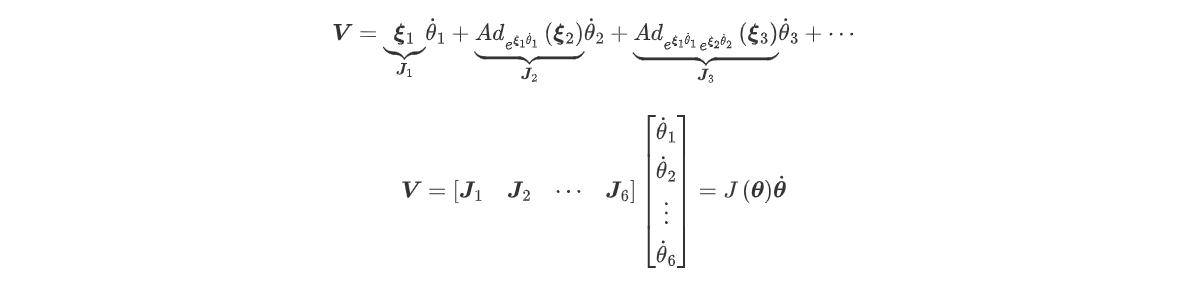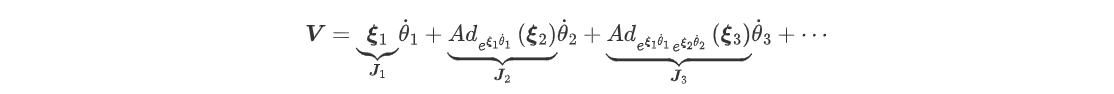一、机器人学
1.1 空间形位与齐次变换
机器人在空间的位姿通常有两种表达方式,一种是在笛卡尔空间表示,通过在世界坐标系和机器人末端上建立坐标系,使用笛卡尔坐标描述机器人的位姿;另一种是通过关节空间表示,使用机器人六个关节的角度来描述机器人的形位。
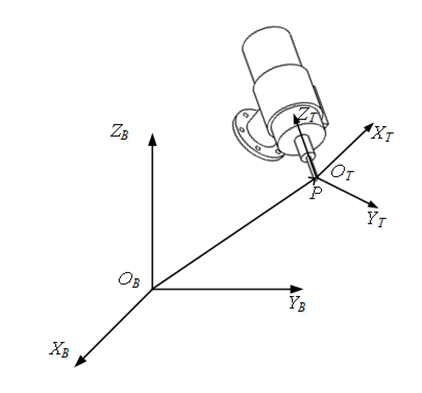
KUKA KR60-3机器人的姿态通常使用笛卡尔坐标进行控制,机器人基坐标系为XB-YB-ZB ,在机器人刀尖上建立工具坐标系XT-YT-ZT ,则末端工具在基坐标系中的位姿就可以用XT-YT-ZT 相对于XB-YB-ZB 的位姿描述。工具坐标系在基坐标系的位姿关系可以用一个 的齐次变换矩阵T
T = [ R P 0 1 ] = [ r 11 r 12 r 21 r 22 r 13 p x r 23 p y r 31 r 32 0 0 r 33 p z 0 1 ] \boldsymbol{T}=\left[ \begin{matrix} \boldsymbol{R}& \boldsymbol{P}\\ 0& 1\\\end{matrix} \right] =\left[ \begin{matrix} \begin{matrix} r_{11}& r_{12}\\ r_{21}& r_{22}\\\end{matrix}& \begin{matrix} r_{13}& p_x\\ r_{23}& p_y\\\end{matrix}\\ \begin{matrix} r_{31}& r_{32}\\ 0& 0\\\end{matrix}& \begin{matrix} r_{33}& p_z\\ 0& 1\\\end{matrix}\\\end{matrix} \right]
T = [ R 0 P 1 ] = r 11 r 21 r 12 r 22 r 31 0 r 32 0 r 13 r 23 p x p y r 33 0 p z 1
1.2机器人运动学建模
1.2.1 基于旋量法的运动学建模
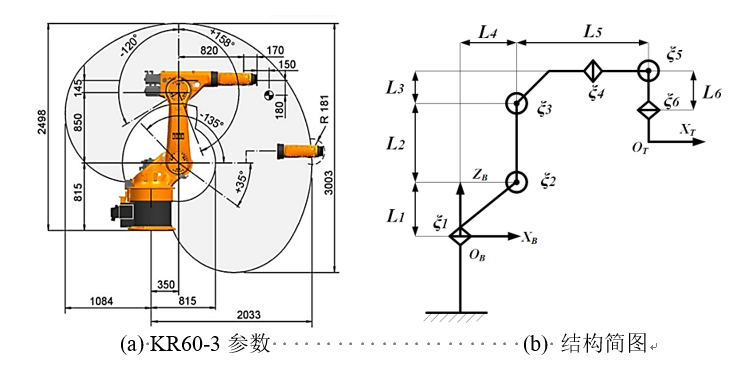
KUKA KR60-3结构简图如图所示,XB-YB-ZB 为基坐标系,XT-YT-ZT 为末端工具坐标系,L 1~L 6为机器人的结构参数,ξ 1 − ξ 6 \boldsymbol{\xi }_1 - \boldsymbol{\xi }_6 ξ 1 − ξ 6 r 1*~r6 分别为关节轴线上任意一点,其中 r4 、r5 、r*6为同一点,即后三关节轴线交点。
在旋量理论中,刚体在笛卡尔空间中的运动速度由角速度ω \omega ω v v v
ξ = [ ω v ] = [ ω − ω × q + h ω ] \boldsymbol{\xi }=\left[ \begin{array}{c} \boldsymbol{\omega }\\ \boldsymbol{v}\\\end{array} \right] =\left[ \begin{array}{c} \boldsymbol{\omega }\\ -\boldsymbol{\omega }\times \boldsymbol{q}+h\boldsymbol{\omega }\\\end{array} \right]
ξ = [ ω v ] = [ ω − ω × q + h ω ]
对于纯转动关节,机器人上一点的形位的变换可以由指数坐标$\boldsymbol{\xi }\theta $表示,也可以将其写为4×4的齐次变换矩阵形式:
T = e [ ξ ] θ = [ e [ ω ] θ ( I θ + ( 1 − cos θ ) [ ω ] + ( θ − sin θ ) [ ω ] 2 ) v 0 1 ] \boldsymbol{T}=e^{\left[ \boldsymbol{\xi } \right] \theta}=\left[ \begin{matrix} e^{\left[ \boldsymbol{\omega } \right] \theta}& \left( \boldsymbol{I}\theta +\left( 1-\cos \!\:\theta \right) \left[ \boldsymbol{\omega } \right] +(\theta -\sin \!\:\theta )\left[ \boldsymbol{\omega } \right] ^2 \right) \boldsymbol{v}\\ 0& 1\\\end{matrix} \right]
T = e [ ξ ] θ = [ e [ ω ] θ 0 ( I θ + ( 1 − cos θ ) [ ω ] + ( θ − sin θ ) [ ω ] 2 ) v 1 ]
e [ ω ] θ = R ( ω , θ ) = I + [ ω ] sin θ + [ ω ] 2 ( 1 − cos θ ) e^{\left[ \boldsymbol{\omega } \right] \theta}=\mathrm{R}\left( \boldsymbol{\omega },\mathrm{\theta} \right) =\mathrm{I}+\left[ \boldsymbol{\omega } \right] \sin \!\:\mathrm{\theta}+\left[ \boldsymbol{\omega } \right] ^2(1-\cos \!\:\theta )
e [ ω ] θ = R ( ω , θ ) = I + [ ω ] sin θ + [ ω ] 2 ( 1 − cos θ )
由机器人的结构参数可以得到机器人的旋量参数,如表所示。
i i i ω i \omega_i ω i q i q_i q i v i v_i v i
1
[0,0,-1]
[0,0,0]
[0,0,0]
2
[0,1,0]
[350,0,815]
[-815,0,350]
3
[0,1,0]
[1200,0,815]
[-815,0,1200]
4
[-1,0,0]
[2020,0,960]
[0,-960,0]
5
[0,1,0]
[2020,0,960]
[-960,0,2020]
6
[-1,0,0]
[2020,0,960]
[0,-960,0]
在KUKA KR60-3工业机器人中,每个连杆通过关节的螺旋运动施加运动给后面的连杆。末端坐标系经由6个关节串联的运动链,做多次螺旋运动,从初始位姿M T
T = e [ ξ 1 ] θ 1 e [ ξ 2 ] θ 2 ⋯ e [ ξ 6 ] θ 6 M \boldsymbol{T}=e^{\left[ \boldsymbol{\xi }_1 \right] \theta _1}e^{\left[ \boldsymbol{\xi }_2 \right] \theta _2}\cdots e^{\left[ \boldsymbol{\xi }_6 \right] \theta _6}\boldsymbol{M}
T = e [ ξ 1 ] θ 1 e [ ξ 2 ] θ 2 ⋯ e [ ξ 6 ] θ 6 M
1.2.2 正运动学代码实现
def Normalize (V ): return V / np.linalg.norm(V) def so3ToVec (so3mat ): return np.array([so3mat[2 ][1 ], so3mat[0 ][2 ], so3mat[1 ][0 ]]) def VecTose3 (V ): return np.r_[np.c_[VecToso3([V[0 ], V[1 ], V[2 ]]), [V[3 ], V[4 ], V[5 ]]], np.zeros((1 , 4 ))] def AxisAng3 (expc3 ): return (Normalize(expc3), np.linalg.norm(expc3)) def MatrixExp3 (so3mat ): omgtheta = so3ToVec(so3mat) if NearZero(np.linalg.norm(omgtheta)): return np.eye(3 ) else : theta = AxisAng3(omgtheta)[1 ] omgmat = so3mat / theta return np.eye(3 ) + np.sin(theta) * omgmat \ + (1 - np.cos(theta)) * np.dot(omgmat, omgmat) def MatrixExp6 (se3mat ): se3mat = np.array(se3mat) omgtheta = so3ToVec(se3mat[0 : 3 , 0 : 3 ]) if NearZero(np.linalg.norm(omgtheta)): return np.r_[np.c_[np.eye(3 ), se3mat[0 : 3 , 3 ]], [[0 , 0 , 0 , 1 ]]] else : theta = AxisAng3(omgtheta)[1 ] omgmat = se3mat[0 : 3 , 0 : 3 ] / theta return np.r_[np.c_[MatrixExp3(se3mat[0 : 3 , 0 : 3 ]), np.dot(np.eye(3 ) * theta \ + (1 - np.cos(theta)) * omgmat \ + (theta - np.sin(theta)) \ * np.dot(omgmat,omgmat), se3mat[0 : 3 , 3 ]) / theta], [[0 , 0 , 0 , 1 ]]] def FKinBody (M, Blist, thetalist ): T = np.array(M) for i in range (len (thetalist)): T = np.dot(T, MatrixExp6(VecTose3(np.array(Blist)[:, i] \ * thetalist[i]))) return T def FKinSpace (M, Slist, thetalist ): T = np.array(M) for i in range (len (thetalist) - 1 , -1 , -1 ): T = np.dot(MatrixExp6(VecTose3(np.array(Slist)[:, i] \ * thetalist[i])), T) return T Slist=np.array([[ 0 , 0 , 0 , -1 , 0 , -1 ], [ 0 , 1 , 1 , 0 , 1 , 0 ], [ -1 , 0 , 0 , 0 , 0 , 0 ], [ 0 , -815 , -815 , 0 , -960 , 0 ], [ 0 , 0 , 0 , -960 , 0 , -960 ], [ 0 , 350 , 1200 , 0 , 2020 , 0 ]]) M=np.array([[ 0 , 0 , 1 , 2190 ], [ 0 , 1 , 0 , 0 ], [-1 , 0 , 0 , 960 ], [ 0 , 0 , 0 , 1 ]]) thetalist=np.array([0 ,-90 /180 *pi,90 /180 *pi,0 ,0 ,0 ]) T = FKinSpace(M,Slist,thetalist)
1.3 基于旋量法的逆运动学求解
1.3.1 PK子问题
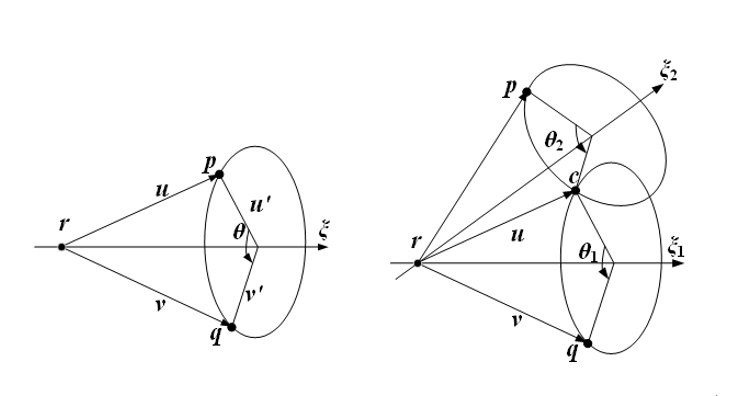
对于六自由度串联机器人而言,逆运动学可以描述成:已知机器人末端工具坐标系位姿,求解满足当前位姿的一组或多组关节角。由KR60-3机器人后三轴相交与一点的特性,利用Paden-Kahan子问题推导机器人关节逆解解析式。Paden-Kahan子问题是基于旋量理论的指数积公式求解各关节旋转角度的几何方法。基于旋量理论的运动学逆解可以分为三个Paden-Kahan子问题,分别是绕单轴旋转、绕两个轴旋转和旋转到给定距离,目前KR60-3的逆运动学求解中只用到了两类子问题,所以本文只介绍子问题1和子问题2,如图所示。
PK子问题1为一个点绕定轴旋转。描述为空间中一点p ξ \boldsymbol{\xi } ξ q θ \theta θ
e [ ξ ] θ p = q e^{\left[ \boldsymbol{\xi } \right] \theta}\boldsymbol{p}=\boldsymbol{q}
e [ ξ ] θ p = q
通过向量之间的几何关系,旋转角θ \theta θ
θ = a tan 2 ( ω T ( u ′ × v ′ ) , u ′ v ′ ) \theta =\mathrm{a}\tan 2(\boldsymbol{\omega }^T\left( \boldsymbol{u}^{\mathrm{'}}\times \boldsymbol{v}^{\mathrm{'}} \right) \text{,}\boldsymbol{u}^{\mathrm{'}}\boldsymbol{v}^{\mathrm{'}})
θ = a tan 2 ( ω T ( u ′ × v ′ ) , u ′ v ′ )
PK子问题2为一个点绕两个相交轴连续旋转。描述为空间中一点p ξ 1 \boldsymbol{\xi }_1 ξ 1 ξ 2 \boldsymbol{\xi }_2 ξ 2 p ξ 2 \boldsymbol{\xi }_2 ξ 2 θ 2 \theta_2 θ 2 s ξ 1 \boldsymbol{\xi }_1 ξ 1 θ 1 \theta_1 θ 1 q ω 1 \omega_1 ω 1 ω 2 \omega_2 ω 2 ξ 1 \boldsymbol{\xi }_1 ξ 1 ξ 2 \boldsymbol{\xi }_2 ξ 2 u = p − r \boldsymbol{u}=\boldsymbol{p}-\boldsymbol{r} u = p − r v = q − r \boldsymbol{v}=\boldsymbol{q}-\boldsymbol{r} v = q − r z = s − r \boldsymbol{z}=\boldsymbol{s}-\boldsymbol{r} z = s − r
e [ ξ 1 ] θ 1 u = z = e − [ ξ 2 ] θ 2 v e^{\left[ \boldsymbol{\xi }_1 \right] \theta _1}\boldsymbol{u}=\boldsymbol{z}=e^{-\left[ \boldsymbol{\xi }_2 \right] \theta _2}\boldsymbol{v}
e [ ξ 1 ] θ 1 u = z = e − [ ξ 2 ] θ 2 v
若两个旋转轴重合,问题就变成了PK子问题1,若两个旋转轴不重合,可通过几何关系求解出中间点z
{ z = a ω 1 + b ω 2 + c ( ω 1 × ω 2 ) a = ( ω 1 T ω 2 ) ω 2 T u − ω 1 T v ( ω 1 T ω 2 ) 2 − 1 b = ( ω 1 T ω 2 ) ω 1 T v − ω 2 T u ( ω 1 T ω 2 ) 2 − 1 c = ∥ u ∥ 2 − a 2 − b 2 − 2 a b ω 1 T ω 2 ∥ ω 1 × ω 2 ∥ 2 \begin{cases} \boldsymbol{z}=a\boldsymbol{\omega }_1+b\boldsymbol{\omega }_2+c\left( \boldsymbol{\omega }_1\times \boldsymbol{\omega }_2 \right)\\ a=\frac{\left( \boldsymbol{\omega }_{1}^{T}\boldsymbol{\omega }_2 \right) \boldsymbol{\omega }_{2}^{T}\boldsymbol{u}-\boldsymbol{\omega }_{1}^{T}\boldsymbol{v}}{\left( \boldsymbol{\omega }_{1}^{T}\boldsymbol{\omega }_2 \right) ^2-1}\\ b=\frac{\left( \boldsymbol{\omega }_{1}^{T}\boldsymbol{\omega }_2 \right) \boldsymbol{\omega }_{1}^{T}\boldsymbol{v}-\boldsymbol{\omega }_{2}^{T}\boldsymbol{u}}{\left( \boldsymbol{\omega }_{1}^{T}\boldsymbol{\omega }_2 \right) ^2-1}\\ c=\frac{\left\| \boldsymbol{u} \right\| ^2-a^2-b^2-2ab\boldsymbol{\omega }_{1}^{T}\boldsymbol{\omega }_2}{\left\| \boldsymbol{\omega }_1\times \boldsymbol{\omega }_2 \right\| ^2}\\\end{cases}
⎩ ⎨ ⎧ z = a ω 1 + b ω 2 + c ( ω 1 × ω 2 ) a = ( ω 1 T ω 2 ) 2 − 1 ( ω 1 T ω 2 ) ω 2 T u − ω 1 T v b = ( ω 1 T ω 2 ) 2 − 1 ( ω 1 T ω 2 ) ω 1 T v − ω 2 T u c = ∥ ω 1 × ω 2 ∥ 2 ∥ u ∥ 2 − a 2 − b 2 − 2 ab ω 1 T ω 2
1.3.2 KUKA KR60-3逆运动学求解
由螺旋理论可知,位于螺旋轴上的点q \boldsymbol{q} q e [ ξ ] θ q = q e^{[\boldsymbol{\xi }]\theta}\boldsymbol{q}=\boldsymbol{q} e [ ξ ] θ q = q q 4 \boldsymbol{q}_4 q 4 q 4 \boldsymbol{q}_4 q 4
T M − 1 q 6 = e [ ξ 1 ] θ 1 e [ ξ 2 ] θ 2 ⋯ e [ ξ 6 ] θ 6 q 4 = e [ ξ 1 ] θ 1 e [ ξ 2 ] θ 2 e [ ξ 3 ] θ 3 q 4 = [ p x , p y , p z , 1 ] \boldsymbol{TM}^{-1}\boldsymbol{q}_6=e^{\left[ \boldsymbol{\xi }_1 \right] \theta _1}e^{\left[ \boldsymbol{\xi }_2 \right] \theta _2}\cdots e^{\left[ \boldsymbol{\xi }_6 \right] \theta _6}\boldsymbol{q}_4=e^{\left[ \boldsymbol{\xi }_1 \right] \theta _1}e^{\left[ \boldsymbol{\xi }_2 \right] \theta _2}e^{\left[ \boldsymbol{\xi }_3 \right] \theta _3}\boldsymbol{q}_4=[p_x,p_y,p_z,1]
TM − 1 q 6 = e [ ξ 1 ] θ 1 e [ ξ 2 ] θ 2 ⋯ e [ ξ 6 ] θ 6 q 4 = e [ ξ 1 ] θ 1 e [ ξ 2 ] θ 2 e [ ξ 3 ] θ 3 q 4 = [ p x , p y , p z , 1 ]
上式表示腕部中心点q 4 \boldsymbol{q}_4 q 4 q 4 \boldsymbol{q}_4 q 4 p 1 \boldsymbol{p}_1 p 1
其中,上述公式中y 2 y_2 y 2 x 2 x_2 x 2 y 3 y_{3} y 3 x 3 x_3 x 3
在得到前三个关节的关节角后,将上一步求取的前三个关节带入公式(2-10)中,然后在原公式中取在轴6上但不在4、5轴上一点进行解耦,即可消除第六轴的影响,将后三轴转换为一个子问题2和一个子问题1进行求解,在公式两边同乘以在轴6上但不在4、5轴上一点p 6 = [ L 4 + L 5 , 0 , 0 ] \boldsymbol{p}_6=[L_4+L_5,0,0] p 6 = [ L 4 + L 5 , 0 , 0 ]
e − [ ξ 3 ] θ 3 e − [ ξ 2 ] θ 2 e − [ ξ 1 ] θ 1 T M − 1 p 6 = e [ ξ 4 ] θ 4 e [ ξ 5 ] θ 5 p 6 = [ q 6 x , q 6 y , q 6 z , 1 ] = q 6 e^{-\left[ \boldsymbol{\xi }_3 \right] \theta _3}e^{-\left[ \boldsymbol{\xi }_2 \right] \theta _2}e^{-\left[ \boldsymbol{\xi }_1 \right] \theta _1}\boldsymbol{TM}^{-1}\boldsymbol{p}_6=e^{\left[ \boldsymbol{\xi }_4 \right] \theta _4}e^{\left[ \boldsymbol{\xi }_5 \right] \theta _5}\boldsymbol{p}_6=\left[ q_{6x},q_{6y},q_{6z},1 \right] =\boldsymbol{q}_6
e − [ ξ 3 ] θ 3 e − [ ξ 2 ] θ 2 e − [ ξ 1 ] θ 1 TM − 1 p 6 = e [ ξ 4 ] θ 4 e [ ξ 5 ] θ 5 p 6 = [ q 6 x , q 6 y , q 6 z , 1 ] = q 6
上式可以看成一个子问题2,p 6 \boldsymbol{p}_6 p 6 p 5 \boldsymbol{p}_5 p 5 q 6 \boldsymbol{q}_6 q 6 q 4 \boldsymbol{q}_4 q 4 p 5 \boldsymbol{p}_5 p 5 θ 4 \theta _4 θ 4 θ 5 \theta _5 θ 5 p 7 = [ L 4 + L 5 + 1 , 0 , 0 ] \boldsymbol{p}_7=[L_4+L_5+1,0,0] p 7 = [ L 4 + L 5 + 1 , 0 , 0 ] 7=\left[ q {7x},q_{7y},q_{7z} \right] ,根据旋量理论将公式进行解耦,即可求出关节角 ,根据旋量理论将公式进行解耦,即可求出关节角 ,根据旋量理论将公式进行解耦,即可求出关节角 ,关节角 ,关节角 ,关节角 、 、 、 、 、 、
{ θ 4 = a tan 2 ( ± q 6 y , ± ( q 6 y − L 1 − L 2 − L 3 ) ) θ 5 = a tan 2 ( ± ( L 1 + L 2 + L 3 ) 2 − ( q 6 x − L 4 − L 5 ) 2 , q 6 x − L 4 − L 5 ) θ 6 = a tan 2 ( q 7 y , L 1 + L 2 + L 3 − q 7 z ) \begin{cases} \theta _4=\mathrm{a}\tan 2\left( \pm q_{6y},\pm \left( q_{6y}-L_1-L_2-L_3 \right) \right)\\ \theta _5=\mathrm{a}\tan 2\left( \pm \sqrt{\left( L_1+L_2+L_3 \right) ^2-\left( q_{6x}-L_4-L_5 \right) ^2},q_{6x}-L_4-L_5 \right)\\ \theta _6=\mathrm{a}\tan 2\left( q_{7y},L_1+L_2+L_3-q_{7z} \right)\\\end{cases}
⎩ ⎨ ⎧ θ 4 = a tan 2 ( ± q 6 y , ± ( q 6 y − L 1 − L 2 − L 3 ) ) θ 5 = a tan 2 ( ± ( L 1 + L 2 + L 3 ) 2 − ( q 6 x − L 4 − L 5 ) 2 , q 6 x − L 4 − L 5 ) θ 6 = a tan 2 ( q 7 y , L 1 + L 2 + L 3 − q 7 z )
1.3.3 基于旋量法的逆运动学数值求解
如果逆运动学方程无解析解时,可采用迭代数值方法求解。即使存在解析解,数值算法也经常用于改善求解的精度。
许多迭代方法可用于非线性方程的求解,’而是将运动学逆解方程转换成现有数值方法可解的形式。为此,将多次使用求解非线性方程的基本方法:牛顿-拉夫森法。此外,也将引入其他一些优化方法,以应对精确解不存在的情况,并利用这些方法得到最接近真实值的解或者相反情况,存在无穷多个运动学逆解(例如,运动学冗余情况)。为此,需要找到相对某种指标的最优解。因此, 下面首先讨论用于求解非线性方程的牛顿-拉夫森法,接下来讨论优化第一必要条件。
(1)牛顿-拉夫森法
对于给定的微分方程方程g g g g ( θ ) = 0 g(\theta)=0 g ( θ ) = 0 θ 0 \theta^0 θ 0 θ 0 \theta^0 θ 0
若只保留到第—阶,令g ( θ ) = 0 g(\theta)=0 g ( θ ) = 0 θ \theta θ
再将上式求得的值作为初值,代人上述方程中,重复求解,得到下述方程:
上述过程不断迭代,直到满足某个指标值。例如,给定预先设定好的阂值满足:
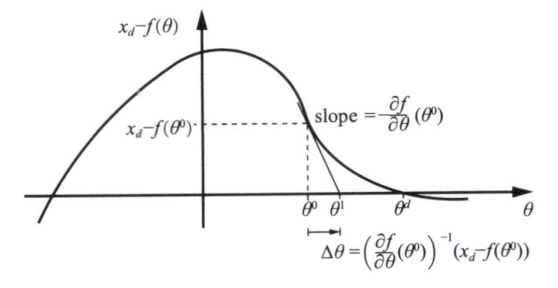
对于KUKA KR60-3六自由度串联机器人,假设我们用坐标向量x x x x = f ( θ ) x = f(\theta) x = f ( θ ) 6 6 6 6 6 6 x d x_d x d g ( θ ) g(\theta) g ( θ ) g ( θ ) = x d − f ( θ ) g(\theta)=x_d - f(\theta) g ( θ ) = x d − f ( θ ) θ d \theta_d θ d
g ( θ ) = x d − f ( θ ) = 0 g(\theta)=x_d - f(\theta)=0
g ( θ ) = x d − f ( θ ) = 0
已知初始估计值θ 0 \theta^0 θ 0 θ d \theta_d θ d
x d = f ( θ 0 ) + J ( θ 0 ) Δ ( θ ) + h . o . t x_d=f(\theta^0)+J(\theta^0)\Delta(\theta) + \mathrm{h.o.t}
x d = f ( θ 0 ) + J ( θ 0 ) Δ ( θ ) + h.o.t
截取泰勒展开第一项,假设J ( θ 0 ) J(\theta^0) J ( θ 0 ) Δ θ \Delta\theta Δ θ
Δ θ = J − 1 ( θ 0 ) ( x d − f ( θ 0 ) ) \Delta\theta=J^{-1}(\theta^{0})(x_{d}-f(\theta^{0}))
Δ θ = J − 1 ( θ 0 ) ( x d − f ( θ 0 ))
若正向运动学是θ \theta θ θ 0 = t h e t a 0 + Δ θ \theta^0 = theta^0 + \Delta\theta θ 0 = t h e t a 0 + Δ θ x d = f ( θ 1 ) x_d=f(\theta^1) x d = f ( θ 1 ) θ \theta θ θ 1 \theta^1 θ 1 θ 0 \theta^0 θ 0 θ d \theta_d θ d
(2)逆运动学的数值算法
实际上,由于计算效率等原因,经常不采用求逆J − 1 ( θ 0 ) J^{-1}(\theta^0) J − 1 ( θ 0 ) A x = b Ax=b A x = b x x x A A A A A A L U LU LU x x x J − 1 J^{-1} J − 1 Moore-Penrose伪逆形式J + J^+ J +
修改上述算法,使之能应用在预期末端位形为T s d ∈ S E ( 3 ) T_{sd}\in SE(3) T s d ∈ SE ( 3 ) x d x_d x d J J J J b J_b J b e = x d − f ( θ i ) e=x_d -f(\theta^i) e = x d − f ( θ i ) T s d − T s d ( θ i ) T_{sd}-T_{sd}(\theta^i) T s d − T s d ( θ i ) J s J_s J s V b ∈ R 6 V_b \in \R^6 V b ∈ R 6 e = x d − f ( θ i ) e=x_d -f(\theta^i) e = x d − f ( θ i ) f ( θ i ) f(\theta^i) f ( θ i ) x d x_d x d T s d ( θ i ) ) T_{sd}(\theta^i)) T s d ( θ i )) T s d T_{sd} T s d
为找到这个V b V_b V b
T b d ( θ i ) = T s b − 1 ( θ i ) T s d = T b s ( θ i ) T s d T_{bd}(\theta^{i})=T_{s b}^{-1}(\theta^{i})T_{s d}=T_{bs}(\theta^{i})T_{s d}
T b d ( θ i ) = T s b − 1 ( θ i ) T s d = T b s ( θ i ) T s d
然后,利用矩阵对数确定[ V ] [V] [ V ]
[ V b ] = l o g T b d ( θ i ) [ V s ] = [ A d T s b ] [ V b ] [V_b]=logT_{bd}(\theta^i)\\
[V_s] = [Ad_{T_{sb}}][V_b]
[ V b ] = l o g T b d ( θ i ) [ V s ] = [ A d T s b ] [ V b ]
由此可以给出逆运动学算法:
(a)初始化:已知T s d T_{sd} T s d θ 0 \theta_0 θ 0 i = 0 i=0 i = 0
(b)计算[ V ] [V] [ V ] ∣ ∣ ω ∣ ∣ > ε ω ||\omega|| > \varepsilon_{\omega} ∣∣ ω ∣∣ > ε ω ∣ ∣ V ∣ ∣ > ε v ||V|| > \varepsilon_{v} ∣∣ V ∣∣ > ε v
计算θ i + 1 = θ i + J + ( θ i ) V \theta^{i+1} = \theta^{i} + J^+(\theta ^ i)V θ i + 1 = θ i + J + ( θ i ) V
i = i + 1 i = i+1 i = i + 1
完成一定次数的迭代后,就都能获得真实值θ d \theta_d θ d θ k \theta^k θ k
(3) 数值解代码实现
def IKinBody (Blist, M, T, thetalist0, eomg, ev ): thetalist = np.array(thetalist0).copy() i = 0 maxiterations = 20 Vb = se3ToVec(MatrixLog6(np.dot(TransInv(FKinBody(M, Blist, \ thetalist)), T))) err = np.linalg.norm([Vb[0 ], Vb[1 ], Vb[2 ]]) > eomg \ or np.linalg.norm([Vb[3 ], Vb[4 ], Vb[5 ]]) > ev while err and i < maxiterations: thetalist = thetalist \ + np.dot(np.linalg.pinv(JacobianBody(Blist, \ thetalist)), Vb) i = i + 1 Vb \ = se3ToVec(MatrixLog6(np.dot(TransInv(FKinBody(M, Blist, \ thetalist)), T))) err = np.linalg.norm([Vb[0 ], Vb[1 ], Vb[2 ]]) > eomg \ or np.linalg.norm([Vb[3 ], Vb[4 ], Vb[5 ]]) > ev return (thetalist, not err) def IKinSpace (Slist, M, T, thetalist0, eomg, ev ): thetalist = np.array(thetalist0).copy() i = 0 maxiterations = 20 Tsb = FKinSpace(M,Slist, thetalist) Vs = np.dot(Adjoint(Tsb), \ se3ToVec(MatrixLog6(np.dot(TransInv(Tsb), T)))) err = np.linalg.norm([Vs[0 ], Vs[1 ], Vs[2 ]]) > eomg \ or np.linalg.norm([Vs[3 ], Vs[4 ], Vs[5 ]]) > ev while err and i < maxiterations: thetalist = thetalist \ + np.dot(np.linalg.pinv(JacobianSpace(Slist, \ thetalist)), Vs) i = i + 1 Tsb = FKinSpace(M, Slist, thetalist) Vs = np.dot(Adjoint(Tsb), \ se3ToVec(MatrixLog6(np.dot(TransInv(Tsb), T)))) err = np.linalg.norm([Vs[0 ], Vs[1 ], Vs[2 ]]) > eomg \ or np.linalg.norm([Vs[3 ], Vs[4 ], Vs[5 ]]) > ev return (thetalist, not err) eomg = 0.01 ev = 0.01 initial = np.array([40.050000 , -50.910000 , 110.140000 , 120.540000 , -11.390000 , 97.930000 ])/180 *math.pi T = np.array([ [0.410150 , -0.123729 , -0.903586 , 1183.631143 ] , [-0.190306 , -0.980556 , 0.047886 , -1137.765860 ] , [-0.891942 , 0.152317 , -0.425722 , 756.413634 ], [ 0.000000 , 0.000000 , 0.000000 , 1.000000 ] ]) [theta,success] = mr.IKinSpace(Slist,M,T,initial,eomg,ev)
1.4 机器人运动学
1.4.1 雅可比矩阵
除了关节角度和机器人末端执行器位置之间的关系外,还需要研究关节和末端执行器速度之间的关系。在本节中,推导了这种关系的公式,并研究其结构和性质,还研究了连杆之间力传递的关系。由第2章的公式(2-5),当给定一组关节角θ = [ θ 1 , θ 2 , θ 3 , θ 4 , θ 5 , θ 6 ] T \boldsymbol{\theta }=\left[ \theta _1,\theta _2,\theta _3,\theta _4,\theta _5,\theta _6 \right] ^{\mathrm{T}} θ = [ θ 1 , θ 2 , θ 3 , θ 4 , θ 5 , θ 6 ] T
X = F ( θ ) \boldsymbol{X}=F\left( \boldsymbol{\theta } \right)
X = F ( θ )
其中,X = [ X , Y , Z , A , B , C ] T \boldsymbol{X}=\left[ X,Y,Z,A,B,C \right] ^{\mathrm{T}} X = [ X , Y , Z , A , B , C ] T
V = X ˙ = J ( θ ) θ ˙ \boldsymbol{V}=\dot{\boldsymbol{X}}=\boldsymbol{J}\left( \boldsymbol{\theta } \right) \dot{\boldsymbol{\theta}}
V = X ˙ = J ( θ ) θ ˙
式中,$\boldsymbol{J}\left( \boldsymbol{\theta } \right) $为雅可比矩阵。
一般情况下,雅可比矩阵通过矢量差乘积法、微分变换法得到。而使用指数积公式表示正运动学,可以更加明确、优雅的推导出雅可比矩阵。在机器人正运动学的指数积公式下,末端的速度$\left[ \boldsymbol{V} \right] $的表达式为:
带入机器人正运动学公式,并使用伴随映射将上式写成向量形式,即:
式中,对于任意ξ ∈ R 6 \boldsymbol{\xi }\in \boldsymbol{R}^6 ξ ∈ R 6
ξ ′ = A d T ( ξ ) = [ R 0 [ P ] R R ] ξ \boldsymbol{\xi }^{\prime}=Ad_{\boldsymbol{T}}\left( \boldsymbol{\xi } \right) =\left[ \begin{matrix} \boldsymbol{R}& 0\\ \left[ \boldsymbol{P} \right] \boldsymbol{R}& \boldsymbol{R}\\\end{matrix} \right] \boldsymbol{\xi }
ξ ′ = A d T ( ξ ) = [ R [ P ] R 0 R ] ξ
1.4.2 雅可比矩阵代码实现
def JacobianBody (Blist, thetalist ): Jb = np.array(Blist).copy().astype(np.float ) T = np.eye(4 ) for i in range (len (thetalist) - 2 , -1 , -1 ): T = np.dot(T,MatrixExp6(VecTose3(np.array(Blist)[:, i + 1 ] \ * -thetalist[i + 1 ]))) Jb[:, i] = np.dot(Adjoint(T), np.array(Blist)[:, i]) return Jb def JacobianSpace (Slist, thetalist ): Js = np.array(Slist).copy().astype(np.float ) T = np.eye(4 ) for i in range (1 , len (thetalist)): T = np.dot(T, MatrixExp6(VecTose3(np.array(Slist)[:, i - 1 ] \ * thetalist[i - 1 ]))) Js[:, i] = np.dot(Adjoint(T), np.array(Slist)[:, i]) return Js
1.5 涉及的函数说明
1.5.1 空间变换与齐次矩阵
1. 计算旋转矩阵的逆invR = RotInv(R) 2. 将三维向量转换为3 *3 反对称矩阵so3mat = VecToso3(omg) 3. 将3 *3 反对称矩阵转换为三维向量omg = so3ToVec(so3mat) 4. 从旋转的三维指数坐标中提取出轴线和角度[omghat,theta] = AxisAng3(expc3) 5. 计算矩阵指数对应的旋转矩阵R = MatrixExp3(so3mat) 6. 计算旋转矩阵对应的矩阵对数so3mat = MatrixLog3(R) 7. M到SO(3 )旋转矩阵的空间距离的度量d = DistanceToSO3(mat) 8. 判断M是否为旋转矩阵judge = TestIfSO3(mat) 9. 返回与M最近的旋转矩阵R = ProjectToSO3(mat) 10. 将旋转矩阵和位置向量转换为变换矩阵T = RpToTrans(R,p) 11. 从变换矩阵中分离出旋转矩阵和位置向量[R,p] = TransToRp(T) 12. 变换矩阵求逆invT = TransInv(T) 13. 构造与六维向量形式的运动旋量V对应的se3mat = VecTose3(V) 14. 构造与se(3 )矩阵对应的六维向量形式的运动旋量VV = se3ToVec(se3mat) 15. 计算变换矩阵T的6 *6 的伴随矩阵AdT = Adjoint(T) 16. 返回正则化的螺旋轴表达式S = ScrewToAxis(q,s,h) 17. 从六位向量形式的指数坐标中提取出螺旋轴和沿轴线移动的距离[S,theta] = AxisAng6(expc6) 18. 计算矩阵指数对应的变换矩阵T = MatrixExp6(se3mat) 19. 计算变换矩阵对应的矩阵对数se3mat = MatrixLog6(T) 20. M到变换矩阵的空间距离d = DistanceToSE3(mat) 21. 判断是否为SE3变换矩阵judge = TestIfSE3(mat) 22. 离M最近的变换矩阵T = ProjectToSE3(mat)
1.5.2 运动学
末端坐标系下。给定初始形位,关节旋量以及关节值,计算末端坐标系 T = FKinBody(M,Blist,thetalist) 空间坐标系下。给定初始形位,关节旋量以及关节值,计算末端坐标系 T = FKinSpace(M,Slist,thetalist) 给定物体坐标系下描述的各关节旋量Blist及关节角,计算物体雅可比JB Jb=JacobianBody(Blist,thetalist) 给定物体坐标系下描述的各关节旋量Slist及关节角,计算物体雅可比Js J=JacobianSpace(Slist,thetalist) [theta11st,success]=IKinBody(B1ist,M,T,theta1ist,eomg,ev) [theta11st,success]=IKinSpace(B1ist,M,T,theta1ist,eomg,ev)
1.6 参考链接
机器人POE运动学代码网址:NxRLab/ModernRobotics: Modern Robotics: Mechanics, Planning, and Control Code Library — The primary purpose of the provided software is to be easy to read and educational, reinforcing the concepts in the book. The code is optimized neither for efficiency nor robustness. (github.com)